来源:Nature自然科研
下一代高性能、低功耗计算机系统的灵感可能来自大脑。不过,随着设计者从传统计算机技术向类脑(神经形态)系统靠拢,他们也必须抛弃支撑传统计算机的已有的形式层次结构,这里的层次结构是一种抽象框架,它从广义上定义了软件如何被数字计算机处理并转换成能在计算机硬件上运行的操作。这种层次结构帮助推动了计算机性能的迅猛发展。张悠慧等人在《自然》发表论文,定义了一种新的层次结构,规范了对算法的要求以及算法在一系列神经形态系统中的实现,为一种结构化的研究方法奠定了基础,从而实现类脑计算机算法和硬件设计的分离。
在过去50年里,传统数字计算机的性能按照摩尔定律一路提升。摩尔定律指出,技术进步大约每18-24个月就会让集成电路(微芯片)的容量翻倍。不过,虽然这些进展带来了越来越强大的硬件,但对于在这些不断变化的器件上执行的算法而言,系统架构师想要优化算法性能面临着不小的挑战。
传统计算机设计有一个重要特征,可以让新器件(芯片、存储器等)实现最佳性能——这个特征就是软硬件开发之间不存在紧耦合。通过对硬件设定最低要求,便可将高级语言写的软件程序转换成任何计算机需要的精确、等价的指令序列——这个过程也称为编译(图1)。在编译过程中,支持使用表示基本计算操作的指令的计算机被认为具有图灵完备性(Turing completeness)。因此,软件代码一般只写一次,然后在多个具有图灵完备性的处理器体系结构上进行编译和执行,产生等价结果。
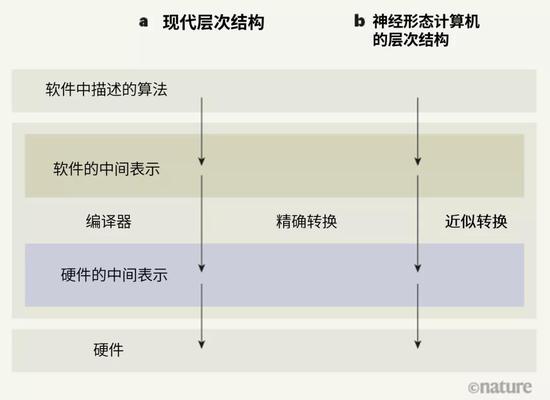
计算机硬件实现算法的层次结构。a,计算机层次结构从广义上定义了软件如何被现代数字计算机处理。用高级计算机语言写的算法被分解成基本计算操作,得到软件的中间表示。这些操作再被转换为精确、等价的硬件中间表示——这组指令随后在硬件上运行。因此,软件可以与硬件分开开发。不过,之前尚未对神经形态计算机(以人工神经元网络为计算基础的计算机)定义过类似的层次结构。b,现在,张悠慧等人[1]提出了一种面向神经形态计算机的类似层次结构。新的层次结构要求硬件中间表示只需近似于软件的中间表示——这克服了神经形态系统产生精确表示所面临的困难。这一层次结构允许神经形态计算机的软硬件分开开发,而不用像现在这样针对每个应用共同开发。
但众所周知的是,摩尔定律定义的进步时代正在走向终结:数字计算机性能的发展速度似乎正在放慢。此外,数字计算有时功耗很大,促使人们寻找替代方案。科学家一直为大脑的计算能力着迷,大脑不仅在能效方面令人惊叹,其神经元和突触的架构也具有独一无二的信息处理性能,让神经形态计算领域深受启发。这个领域以大脑的神经网络架构为基础开发下一代计算机。
神经形态计算一般聚焦脉冲神经网络(spiking neural network,SNN),即互联的人工神经元系统,其中每个神经元在激活水平到达一定阈值后,都会出现短暂的“脉冲”活动。这类系统更接近于生物学上的神经网络,而不是现代深度学习应用所使用的人工神经网络。神经形态硬件已经有各种形式的版本,数字和模拟都有。但是,大部分系统都遵循通用的设计原理,比如存储器和处理器的co-location模式。
神经形态硬件应用开发上的一个挑战在于,尚不存在图灵完备性这样的形式层次结构。恰恰相反,每一种新的芯片体系结构都需要一个自定义软件工具链——一组编程工具——来定义算法并映射到特殊硬件来执行算法。如此一来,研究人员很难比较不同神经形态系统执行同一种算法的性能,而且研究人员还要理解算法和硬件的所有方面,才能获得潜在的类脑性能。
针对这个问题,张悠慧等人想到了一种突破性的解决方法,他们提出了一种他们称之为神经形态完备性(neuromorphic completeness)的概念——呼应了图灵完备性,旨在让算法与硬件开发去耦合。通过放松传统计算机对层次结构的约束,作者提出,如果一个类脑系统能以规定的准确度执行一组给定的基本操作,那么该系统就具备神经形态完备性(图1)。这个概念脱离了图灵完备性——根据图灵完备性,只有当一个系统能对一组给定的基本操作给出精确、等价的结果时,这个系统才能被定义为具有完备性。
在作者提出的神经形态完备性框架中,基本操作包含加权和操作(weighted-sum operation)以及元素对应线性整流操作(element-wise rectified linear operation),这些操作能让硬件系统支持脉冲和非脉冲人工神经网络。作者演示了他们的类脑计算层级结构如何能提供一种机制,将给定算法转换成适合各种神经形态完备器件的形式。
新的层次结构有一大优点,那便是它提出了完备性的连续性(continuum),即不同水平的算法性能都能被接受,具体取决于神经形态系统执行基本操作的准确度。这种完备性的连续性意味着,新的层次结构能用现有的全部模拟和数字神经形态系统来实现,包括那些为了执行速度或能效而牺牲准确度的系统。
完备性的连续性还允许在相同硬件上以不同方式实现同一种算法——比如,用来探索如何用算法准确度换取芯片尺寸,从而降低功耗。张悠慧等人通过执行三项任务的算法(“驾驶”一辆无人自行车、模拟鸟群运动、运行名为QR分解的线性代数分析),演示了他们的方法在这方面的能力。每项任务都用三个典型的神经形态完备性硬件平台来执行:作者自己的神经形态芯片;传统计算机使用的图形处理单元(GPU);一个基于忆阻器、能加速神经网络执行速度的平台。
新提出的层次结构受到了业内欢迎,因为它允许比较同一个算法的等价版本在不同硬件平台的实现结果,以及不同算法在相同硬件上的实现结果。在对神经形态系统结构的有效基准测试中,以上两项任务都非常关键。作者在他们的原理验证实验中囊括了传统的图灵完备硬件(GPU)也很有意义,因为这告诉我们,这种层次结构或能用来证明神经形态器件在特定应用上超过主流系统的优势。

来源:pixabay
新提出的层次结构还有另外一个重大优势,那就是它有望将算法和硬件的开发分割成独立的研究分支。若要解锁神经形态系统结构的潜在优势,算法的规模和复杂度都需要逐渐增加,而这种分割将帮助研究人员聚焦于研究问题的特定方面,而不是想尽办法寻找整个端对端解决方案。这有望增进我们对这些问题的理解,并在将来协助设计更高性能的神经形态系统。
要把神经形态计算领域大量的产业和学术团队的研究工作整合起来,还有很多工作要做。张悠慧等人提出的层次结构在这个方向上迈出了重要一步。真正的大脑——生物学“硬件”——本身是否具有神经形态完备性,仍有待探索;但无论如何,作者的方法让我们与类脑硬件所能带来的巨大效益更近了一点。